​ SRAM PUF 一直是 PUF 设备种类中，较为热门的一个方向，那么对于这一类设备来说如何对其或者说对其产生的密钥和随机数进行评价呢，以下几篇论文都对其进行了阐述。（续接上文-2）

A systematic method to evaluate and compare the performance of physical unclonable functions

​ Embedded systems design with FPGAs, 2013: 245-267.

​ 这篇文章提出了一种系统方法，用于评估和比较物理不可克隆功能（PUF）的性能。文章的主要目的是为现有的多种PUF提供一个公平的、基于统计学的评估框架，因为目前尚没有统一的方法可以比较不同PUF在性能上的优劣。作者提出了三维度的PUF测量方法，并定义了一组评估参数来量化不同PUF的性能。这些参数包括唯一性、可靠性、随机性、稳定性、比特别名效应、扩散性和误识别概率。此外，文章还通过实际数据比较了两种PUF（环形振荡器PUF和仲裁器PUF）的性能表现，验证了所提出方法的有效性。

创新点：

1. 三维度的PUF测量模型：提出了基于设备（设备间区别）、时间（相应可靠性）和空间（随机值取值方式）三个维度的测量方法，全面涵盖了PUF性能评估的关键方面。
2. 紧凑的评估参数集：通过对现有文献的分析，去除了冗余，提出了更紧凑的评估参数集，能更有效地进行不同PUF的比较。
3. 统计学分析的独立性：采用了统计学分析，使该方法能够跨越不同PUF技术的限制，从而实现通用的性能比较。

几个符号表示：

唯一性

​ 唯一性代表了PUF在一组相同类型的芯片中唯一地区分一个特定芯片的能力。

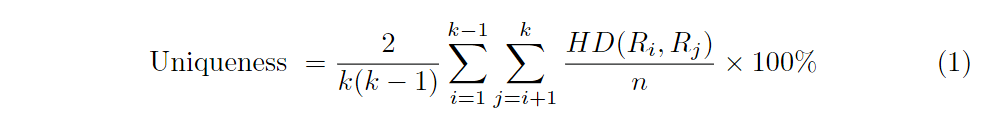
可靠性

​ PUF的可靠性反映了PUF在重现响应位方面的效率。

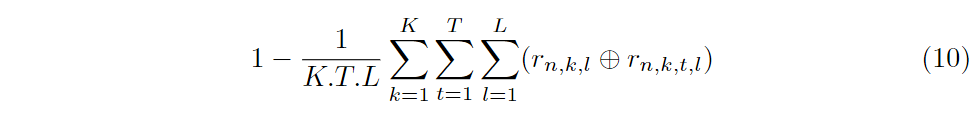
均匀性

​ PUF的均匀性估计了PUF的响应位中discloit0s和scloit1s的比例有多均匀。

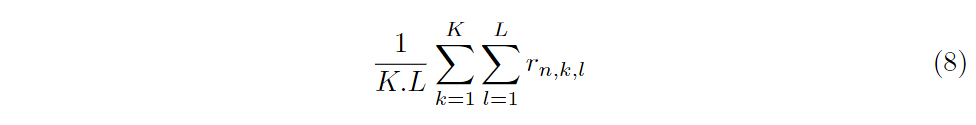
位混叠

​ 如果发生位混叠，不同的芯片可能产生几乎相同的PUF响应，这是一个不理想的效果。

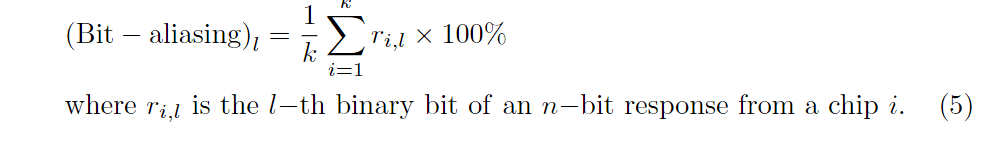
稳定性

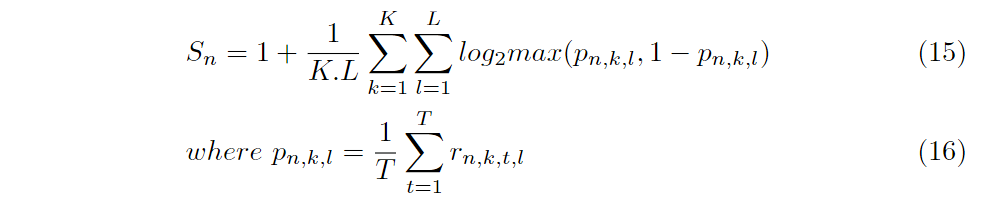
分散性

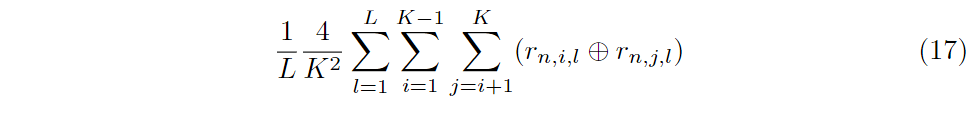
PMSID误识别率

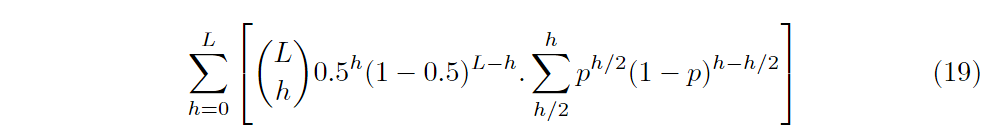
Determining the Quality Metrics for PUFs and Performance Evaluation of Two RO-PUFs

​ 10th IEEE international NEWCAS conference，2012.

​ 物理不可克隆函数（PUF）是一种电路基元，根据制造过程中存在的不可控元件，产生芯片的特定签名。认证、密钥生成和IP保护是PUF电路的三个重要使用领域。除了不可克隆性之外，唯一性和稳健性是每个PUF应该提供的主要属性。尽管文献中提出了许多PUF类型，但这些特性或测试方法的标准和令人满意的性能评估指标还没有被提出。在这项工作中，为了对PUF进行公平和详细的性能评估，已经开发了一套完整的质量指标。其次，提出了一种测试方法，并在PUF评估中采用了置信区间和置信度概念，以保持结果的可靠性。我们在FPGA上实现了两个基于环形振荡器的PUF电路，并根据提出的质量指标详细评估了它们在不同环境条件下的性能。

​ 创新点：尽管存在相当多的不同的PUF结构，并且在文献中提出了结果，但没有对鲁棒性和唯一性进行详细的评估。Hori等人和Maiti等人定义的质量指标，用直接的方法评估了鲁棒性和唯一性。这使得我们无法比较PUF,并为特定的应用选择最佳的拟合结构。同样，也没有定义PUF电路的测试方法，每个PUF都用不同的参数集进行测试，这也阻碍了对电路的有意义的比较。

唯一性

​ 唯一性体现PUF的芯片间差异，在理想情况下，来自不同芯片的所有PUF输出应该是均匀分布和统计上独立的。

1. 汉明距离(U_QM1)

   ​ 如果这组测量值在统计上是独立的，它们的汉明距离（HD）将是50%。

   

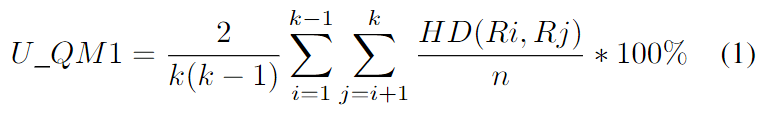
   公式解释：

   • U_QM1 表示唯一性度量值。
   • k表示总的响应序列数。
   • n表示每个响应序列的比特长度。
   • HD(Ri,Rj)表示响应序列 Ri和 Rj之间的汉明距离。
   • 两层求和符号代表对所有可能的响应序列对（Ri和 Rj，其中 i<j）进行累加。

   计算方法：

   1. 计算汉明距离：汉明距离是两个相同长度的二进制序列之间不同位的个数。例如，序列 1010和 1001的汉明距离为 2（第2位和第4位不同）。

   2. 求平均值

      ：通过两两序列之间的汉明距离的平均值衡量唯一性。

      • 首先计算每一对响应序列之间的汉明距离 HD(Ri,Rj)。
      • 然后对所有序列对的汉明距离求和，除以响应序列总数对的数量 k(k−1)\2。
      • 最后除以比特长度 n，并乘以 100%，得到百分比形式的唯一性。

   ​ 即使上述质量指标U_QM1给出了关于系统性能的信息，它也不能保证均匀分布，因为非均匀数据也可能产生50%的HD。如果将第一个质量指标作为唯一的性能参数，两个性能不同的PUF可以被评估为相同。

2. 汉明距离的高斯程度(U_QM2)

   ​ 文章认为PUF数据的HD分布在理想状态下应该与高斯分布相关联，因此通过计算理想分布与实际分布之间的相关系数，结果越接近于1，分布就越高斯；因此电路在唯一性方面表现更好。

   

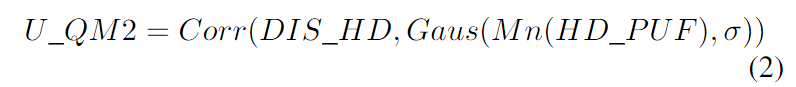
   具体计算方法：

   1. 计算离散汉明距离 (DIS_HD)：
      • 对PUF响应序列进行两两比较，计算汉明距离（HD），这给出了实际观测的汉明距离分布。
   2. 计算PUF响应的平均汉明距离：
      • 计算所有响应序列之间的汉明距离的均值 Mn(HD_PUF)和标准差 σ，得到这组数据的分布特性。
   3. 拟合高斯分布：
      • 基于 Mn(HD_PUF)和 σ参数，生成一个理论上的高斯分布，作为PUF响应序列的理想分布。
   4. 计算相关性：
      • 使用相关性函数 Corr(x,y)，对离散汉明距离分布 DIS_HD和理论高斯分布 Gaus(Mn(HD_PUF),σ)进行相关性分析。
      • 相关性值反映了实际观测汉明距离分布和理论高斯分布的吻合程度。如果相关性较高，则说明PUF响应序列的实际汉明距离分布和理论高斯分布接近。

3. Gilbert-Varshamov bound(U_QM3)

   ​ Gilbert-Varshamov bound（GVB）被用来确定PUF输出对穷举搜索攻击的安全性。这是通过计算均匀分布的输出集合中两个随机输出之间的最小汉明距离来实现的。这个约束也可以用来确定结构的唯一性。

   ​ 在收集了一定数量的数据后，计算出它们之间的最小距离dHm，并通过（3）和（4）确定R’。理想的R是通过（5）使用测量次数M和PUF长度N来计算的。如(6)所示，R与理想R的比例也可以作为唯一性的质量指标U QM3。如果输出是均匀分布的，意味着唯一性是理想的，那么最小HD与GVB兼容，U_QM3趋于统一。否则，最小HD比约束状态差，U_QM3小于1。

   

   ​

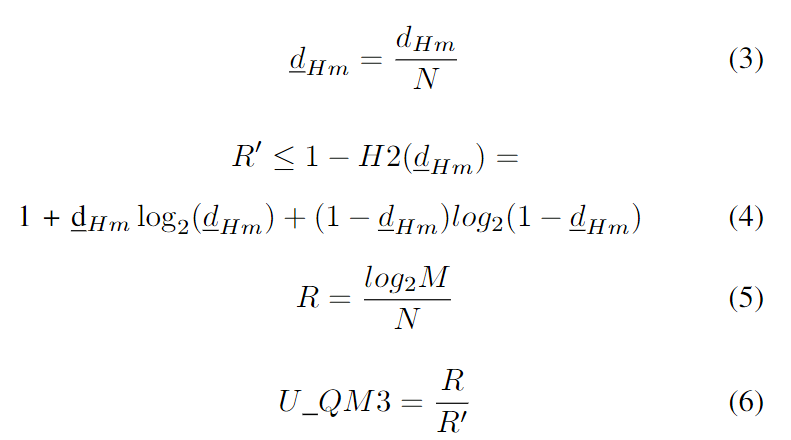
稳定性/鲁棒性

​ 稳健性是指对于性能最好的PUF电路来说，理想情况下应该为零的片内变化。然而，由于环境的变化和结构的内部特征，输出的一些位可能在不同的测量中有所不同。稳健性是通过从单个集成电路中获取一些测量值并计算平均错误率R_QM1来衡量的。

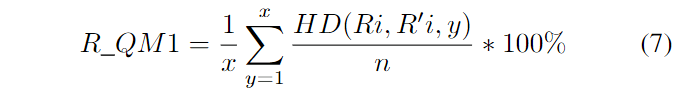
​ 由于某些使用PUF输出的系统需要无误差的数据，因此会利用纠错码来确保每次测量都能产生相同的输出。纠错码的复杂度，以及相应的成本，取决于它们能够纠正的最大错误位数。因此，我们认为对于这些系统来说，平均错误率并不是关键因素。相反，我们可以提出一个新的质量指标，即在一定次数的测量中出现的最大错误率，我们将其定义为R_QM2，它能够衡量系统的鲁棒性，具体内容如公式(8)所示。

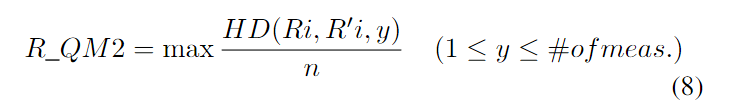
​ 另一组在文献中展示的数据是响应位上错误分布的情况。这些数据被用来掩盖错误最多的位，并计算出改进后的错误率。如果能够方便地检测出每个电路中最有问题的位，并在每次测量后消除它们，这种方法在实践中可能会很有帮助。因此，通过掩盖一定数量的位（在这个案例中是3位）来降低错误率，可以作为PUF电路鲁棒性的另一个质量指标，我们将其称为R_QM3。这个指标的计算方法如公式(9)所示，其中R’_QM1代表掩盖最错误的3位之后的平均错误率。

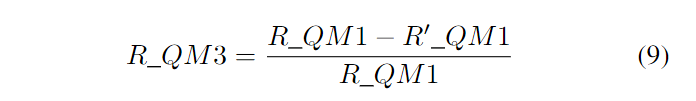
​ 提高PUF电路鲁棒性的一个常用方法是多数投票[10]、[11]。每个输出位都是通过多数投票生成的。这种方法尤其在正常工作条件下提高了鲁棒性。因此，经过多数投票后的平均错误率，R_QM4，也可以作为一个重要的质量指标。这个指标的计算方法如公式(10)所示，其中R”_QM1代表进行了3次多数投票后的平均错误率。

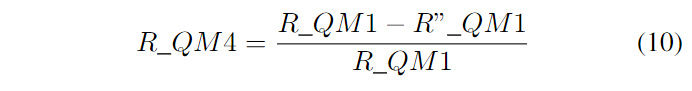
​ 稳定位计数，即在每次测量中都能生成相同输出的位，也是一个重要的参数。如果选择并使用了稳定位，就消除了对纠错码的需求。因此，对于PUF结构来说，稳定位计数，R_QM5，可以作为鲁棒性的质量指标。由于PUF输出非常容易受到环境变化的影响，我们将根据正常工作条件(NOC)和变化温度(VT)下的质量指标来展示结果。

PUF评估的置信区间概念

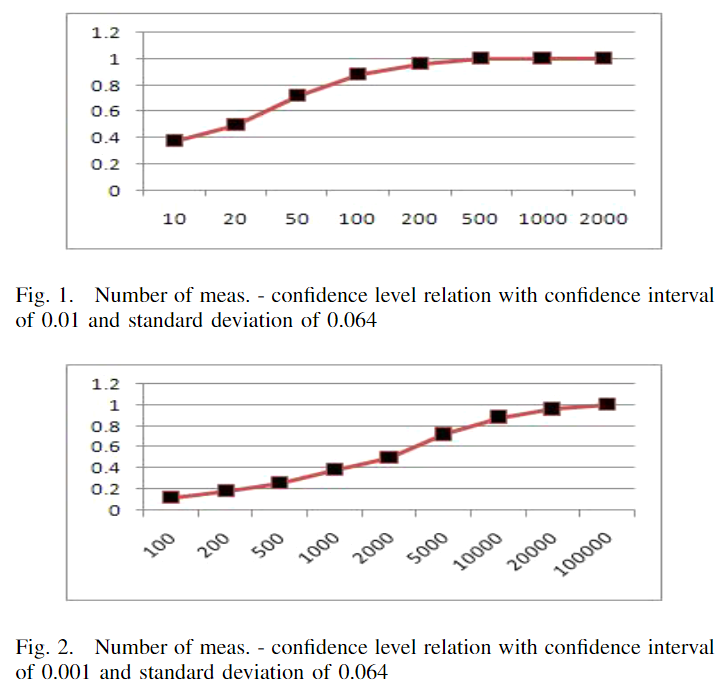
​ 在前面的部分中，我们介绍了将从测量中计算出的质量指标。然而，为了进行可靠的性能评估，需要进行多少次测量仍然是一个值得商榷的问题。因此，为了展示结果的可信度，我们引入了置信区间和置信水平的概念，将其应用于PUF性能评估。在这种方法中，设定置信水平和置信区间来确定必须进行的测量次数。这是通过切比雪夫不等式[12]来计算的，如公式(11)-(14)所示。随着测量次数的增加，置信水平提高和/或置信区间缩小。例如，通过使用1000次测量可以实现99.9%的置信水平和0.1%的置信区间，而25次测量只提供95%的置信水平和2%的置信区间。测量次数、置信区间、置信水平和测量标准差之间的关系在图1和图2中展示。从图表中可以看出，随着测量次数的增加，结果的置信水平提高。第一个图表的置信区间宽了十倍，确保了在测量次数较少的情况下也能获得较高的置信水平。

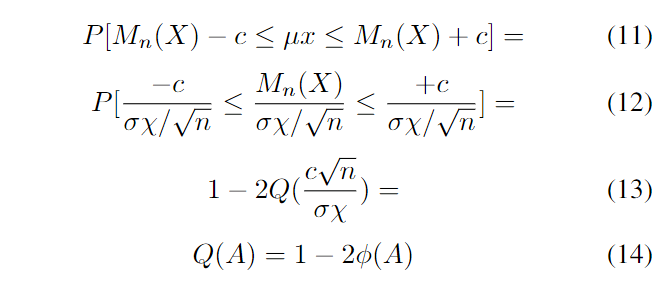
参考文献

[1] Maiti A, Gunreddy V, Schaumont P. A systematic method to evaluate and compare the performance of physical unclonable functions[J]. Embedded systems design with FPGAs, 2013: 245-267.

[2] Kömürcü G, Dündar G. Determining the quality metrics for PUFs and performance evaluation of two RO-PUFs[C]//10th IEEE international NEWCAS conference. IEEE, 2012: 73-76.